mysql为什么使用B+树-能存储多少行
目录
B+树可以存放多少行数据?
先来看B+树可以存放多少行数据。
InnoDB的一棵B+树可以存放多少行数据?
答案:约至少2千万
这是可以算出来的,要搞清楚这个问题,先从InnoDB索引数据结构、数据组织方式说起。
计算机在存储数据的时候,有最小存储单元,这就好比现金的流通最小单位是一毛。
在计算机中,磁盘存储数据最小单元是扇区,一个扇区的大小是512字节,而文件系统(例如XFS/EXT4)的最小单元是块,一个块的大小是4k,而对于InnoDB存储引擎也有自己的最小储存单元,页(Page),一个页的大小是16K。
下面几张图可以理解最小存储单元:
InnoDB的所有数据文件(后缀为ibd的文件),大小始终都是16384(16k)的整数倍。
磁盘扇区、文件系统、InnoDB存储引擎都有各自的最小存储单元。
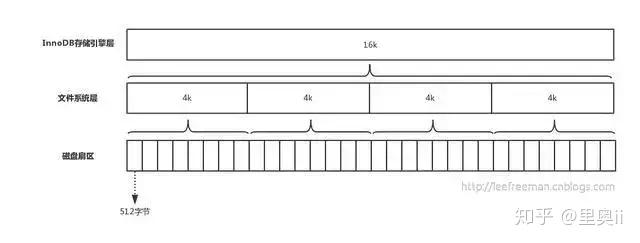
在MySQL中,InnoDB页的大小默认是16k,当然也可以通过参数设置:

表中的数据都是存储在页中的,所以一个页中能存储多少行数据呢?
假设一行数据的大小是1k,那么一个页可以存放16行这样的数据。
如果数据库只按这样的方式存储,如何查找数据就成为一个问题, 因为不知道要查找的数据存在哪个页中,也不可能把所有的页遍历一遍,那样太慢了。
所以伟大的人类找到了B+树的方式来组织这些数据,如图所示:
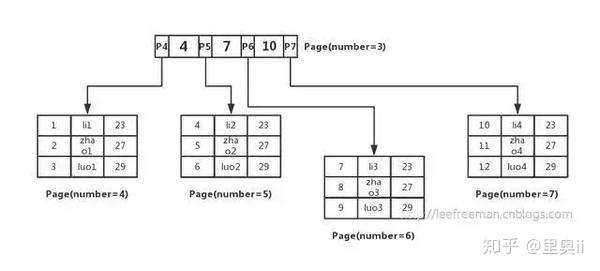
先将数据记录按主键进行排序,分别存放在不同的页中(为了便于理解这里一个页中只存放3条记录,实际情况可以存放很多)
除了存放数据的页以外,还有存放键值+指针的页,如图中page number=3的页,该页存放键值和指向数据页的指针,这样的页由N个键值+指针组成。
当然它也是排好序的。这样的数据组织形式,我们称为索引组织表。
现在来看下,要查找一条数据,怎么查?
如:select * from user where id=5;
这里id是主键,通过这棵B+树来查找,首先找到根页,你怎么知道user表的根页在哪呢?
其实每张表的根页位置在表空间文件中是固定的,即page number=3的页。
找到根页后通过二分查找法,定位到id=5的数据应该在指针P5指向的页中,那么进一步去page number=5的页中查找,同样通过二分查询法即可找到id=5的记录:
| 5 | zhao2 | 27 |
现在清楚了InnoDB中主键索引B+树是如何组织数据、查询数据的。
总结一下:
- InnoDB存储引擎的最小存储单元是页,页可以用于存放数据也可以用于存放键值+指针,在B+树中叶子节点存放数据,非叶子节点存放键值+指针。
- 索引组织表通过非叶子节点的二分查找法以及指针确定数据在哪个页中,进而在去数据页中查找到需要的数据;
叶子结点可以存放多少行数据
那么回到我们开始的问题,通常一棵B+树可以存放多少行数据?
这里我们先假设B+树高为2,即存在一个根节点和若干个叶子节点,那么这棵B+树的存放总记录数为:根节点指针数 * 单个叶子节点记录行数。
上文已经说明单个叶子节点(页)中的记录数=16K/1K=16。(这里假设一行记录的数据大小为1k,实际上现在很多互联网业务数据记录大小通常就是1K左右)。
非叶子结点存放多少指针
那么现在需要计算出非叶子节点能存放多少指针?
其实这也很好算,假设主键ID为bigint类型,长度为8字节,而指针大小在InnoDB源码中设置为6字节,这样一共14字节
我们一个页中能存放多少这样的单元,其实就代表有多少指针,即16384/14=1170。
一颗B+树可存放多少行记录
那么可以算出一棵高度为2的B+树,能存放1170*16=18720条这样的数据记录。
根据同样的原理可以算出一个高度为3的B+树可以存放:1170*1170*16=21902400条这样的记录。
所以在InnoDB中B+树高度一般为1-3层,它就能满足千万级的数据存储。
在查找数据时,一次页的查找代表一次IO,所以通过主键索引查询通常只需要1-3次IO操作即可查找到数据。
mysql为什么使用B+树
有一道MySQL的面试题,为什么MySQL的索引要使用B+树而不是其它树形结构?比如B树?
简单回答是:
因为B树不管叶子节点还是非叶子节点,都会保存数据,这样导致在非叶子节点中能保存的指针数量变少(有些资料也称为扇出)
指针少的情况下要保存大量数据,只能增加树的高度,导致IO操作变多,查询性能变低;
更多了解:漫画B+树 - 9ong
本文收藏来自互联网,仅用于学习研究,著作权归原作者所有,如有侵权请联系删除
markdown 9ong@TsingChan
部分引用格式为收藏注解,比如本句就是注解,非作者原文。
